This was a random pet project from the idea "For a set of randomly distributed points within a rectangle on a 2D plane, find the optimal angle to start movement of one point so that it internally reflects within the rectangle and intersects with the maximum number of other points."
-
Draw a bunch of random points in a rectangle and select one point as your 'cue' ball.
-
Draw a line at a random angle on the cue ball, find the intersection with the wall, and reflect a new line across the perpendicular to that intersection.
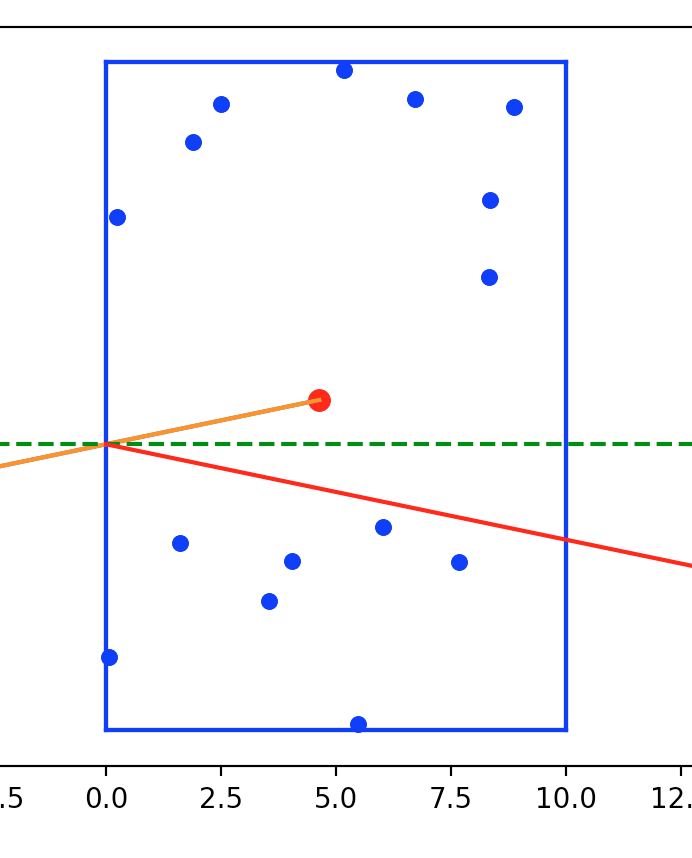
-
With that new line, repeat the process n number of times.
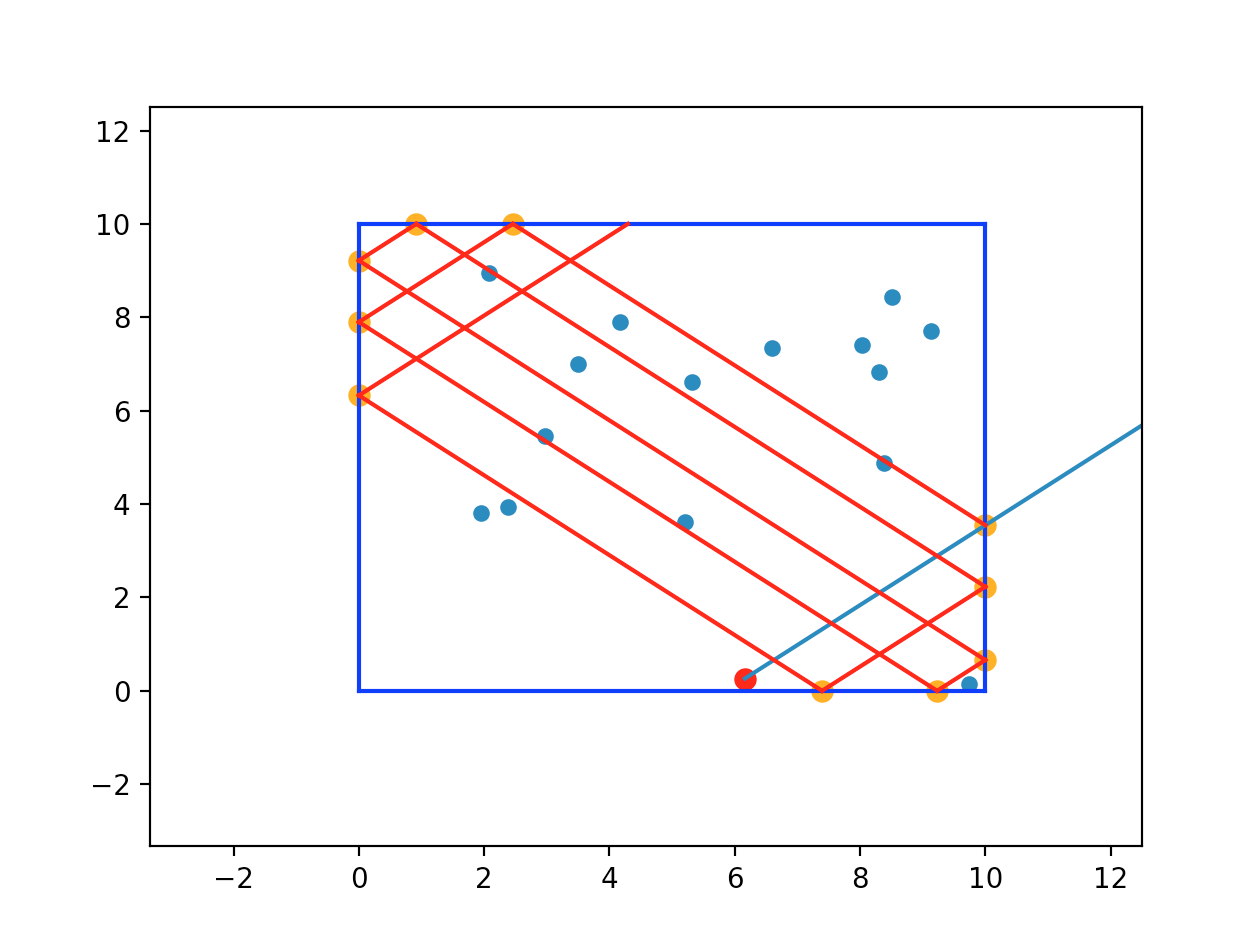
-
Find what points intersect with the lines (with each point having some radius).
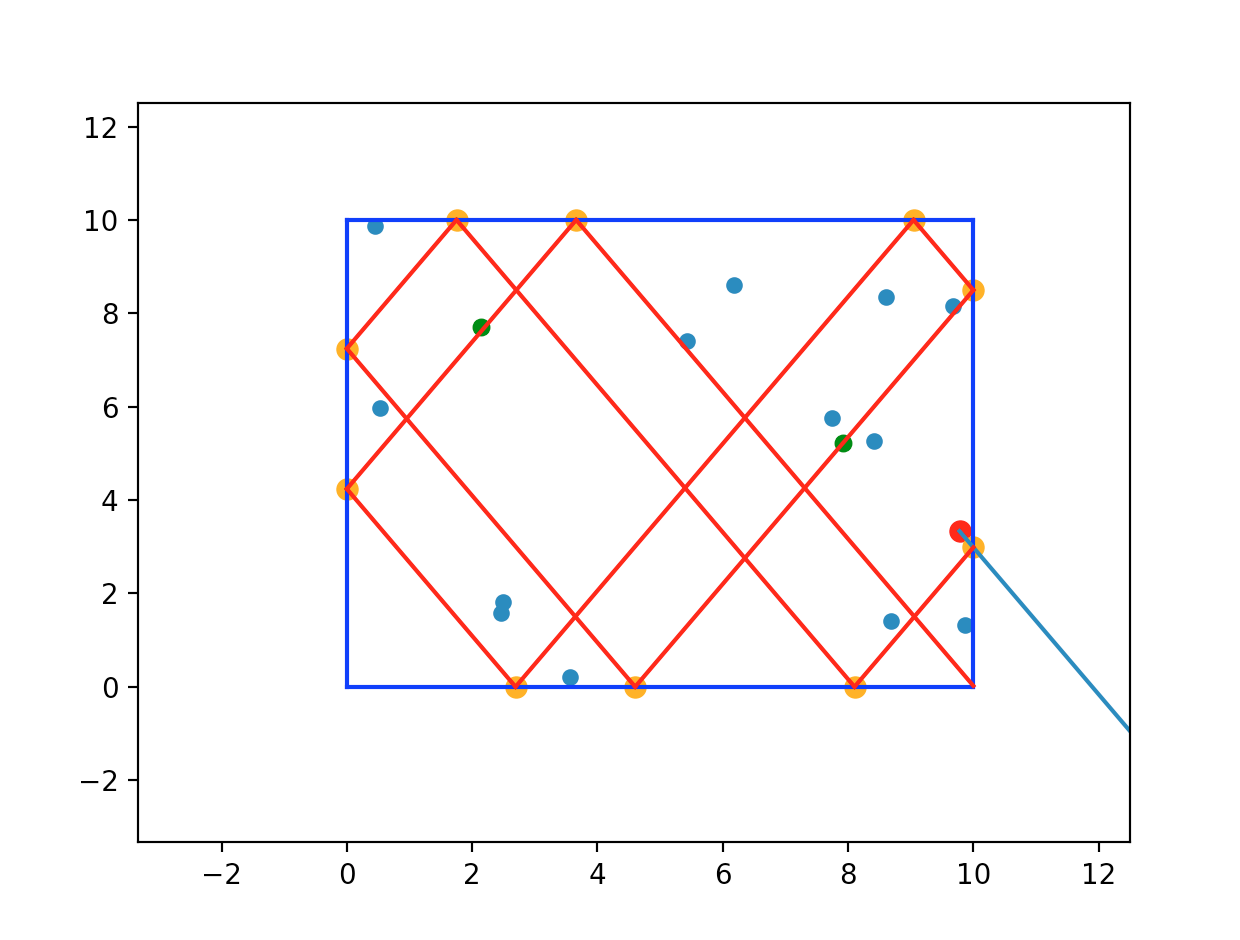
-
For a random set of points and a randomly selected 'cue ball' point, calculate this for every degree in 360 degrees.
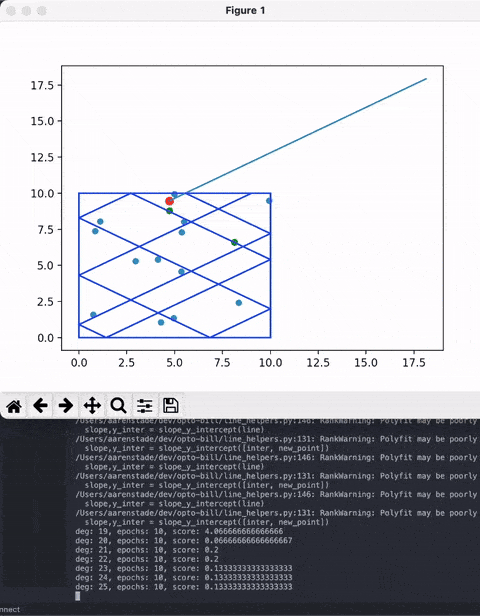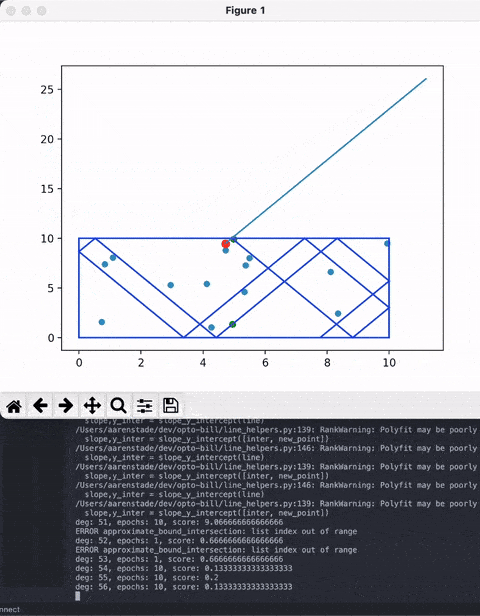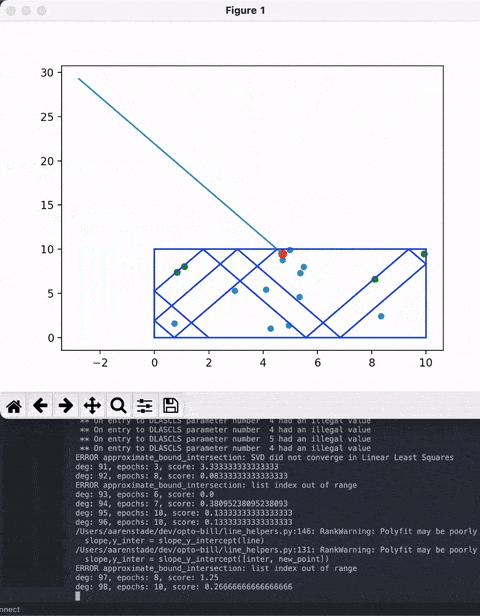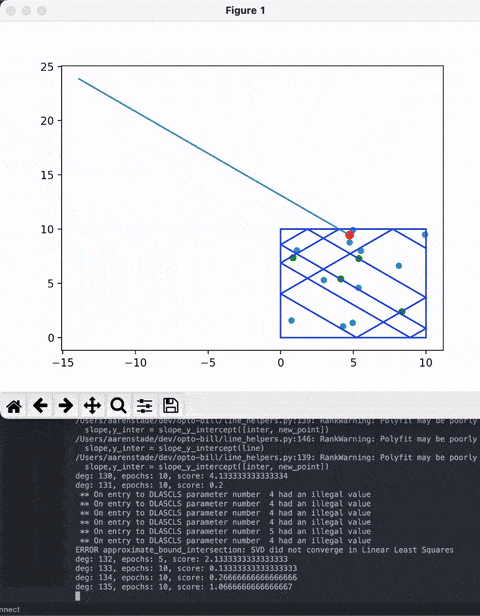
Obviously there are some bugs but it mostly works.
Then, the idea is with all this data you could train a simple model to predict - for any given set of random points and a randomly selected cue ball, what is the optimal angle to hit the most number of other balls.
Other stuff that'd be interesting:
- Calculating reflections based on collisions with other balls.
- Adding some 'physics' or friction to limit the number of reflections.
- Adding basic physics to emulate the movement of other balls.
Was a fun experiment!